PERCENTILOVÁ METODA A METODA SD-SKORE

Percentilová metoda je variantou statistického zpracování dat. Pojmově nejblíže je percentilům střední hodnota (medián), která je 50. percentilem souboru dat. Percentily tvoří dělítka mezi setinami daného souboru, percentilů je tedy devadesátdevět a soubor konkrétních dat je pomocí devadesátidevíti percentilů rozdělen na sto stejných dílů.

Podkladem pro sestrojení tzv. percentilových grafů jsou hodnoty percentilů vypočítané z dat jedinců vyšetřených v rámci reprezentativních referenčních studií. (Např. národní antropometrické průřezové studie se v ČR provádějí od roku 1951 každých deset let a v současnosti jsou v pediatrické praxi u nás používány percentilové grafy antropometrických hodnot z roku 1991, vytvořené z dat 4-5 % populace ČR od 0 do 18 let).

Pásmo širší normy je nejčastěji vymezováno 2. až 98., resp. 3. až 97. percentilem. Mezi těmito krajními hodnotami se nalézá 96 % (resp. 94 %) empiricky zjištěných hodnot daného parametru pro daný věk a pohlaví. Pásmo mezi 25. a 75. percentilem, v němž leží padesát procent všech hodnot, posuzujeme jako pásmo středních hodnot. U parametrů, které mají tzv. normální (gaussovské) rozdělení, je 50. percentil shodný s aritmetickým průměrem.

Nad 75. percentilem jsou jedinci s vyšší až vysokou hodnotou posuzovaného parametru, nad 90. percentilem s velmi vysokou. Pod 25. percentilem jsou hodnoty nižší až nízké, pod 10. percentilem velmi nízké. Při daném pojetí normy jsou tři procenta dětí (s hodnotami nad 97. percentilem) v pásmu vysoce významného nadprůměru a tři procenta dětí (s hodnotami pod 3. percentilem) v pásmu vysoce významného podprůměru.

Po zakreslení zjištěné hodnoty do percentilového grafu je možné okamžitě porovnat hodnotu sledovaného parametru s daty vrstevníků a zhodnotit tak míru odlišnosti od normy. (Př. Dítě s 25.percentilem tělesné výšky je vyšší než čtvrtina jeho vrstevníků, 75 % jeho vrstevníků je však vyšší než toto dítě).

Kvantitativní biomedicínské hodnoty je též možno vyjádřit v tzv. normalizované podobě, s využitím skóre směrodatné odchylky (SD-skóre, SDS). V praxi se toto vyjádření užívá především pro určení míry extrémních odchylek od normy, tedy hodnot z pásem, kam již síť empirických percentilů nezasahuje. Skóre směrodatné odchylky vypočítáme podle vzorce:

SDS = x - X / SD
x = parametr vyšetřeného dítěte
X = tabelovaná průměrná hodnota daného parametru pro daný věk a pohlaví
SD = směrodatná odchylka (Standard Deviation) tabelovaného průměru daného parametru pro daný věk a pohlaví

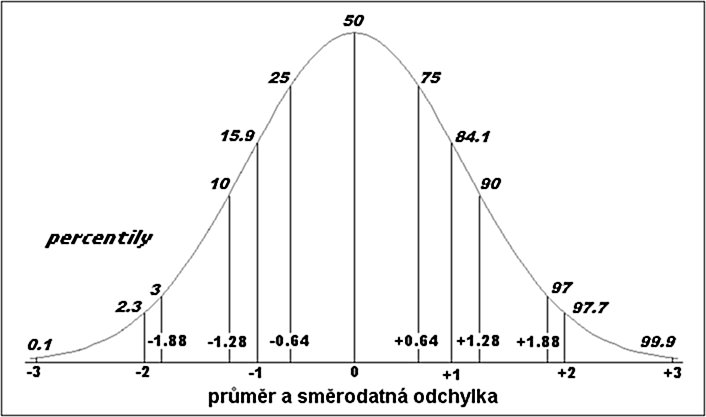
Výpočtem SD-skóre se zodpovídá otázka, o kolik směrodatných odchylek je hodnocený parametr větší či menší než jeho tabelovaná průměrná hodnota. Z definice SDS vyplývá, že např. u dítěte se zcela průměrnou hodnotou tělesné výšky, má SDS jeho výšky hodnotu nula. Dítě, jehož SDS výšky dosahuje +2.0 je výškou na horní hranicí širší normy (přesně na 98.percentilu). Dítě s SDS výšky rovno - 2.0 je na dolní hranici širší normy, resp. na druhém percentilu (viz obr. relace percentilů a SD). SD-skóre se používá např. též při zpracování dat klinických souborů, protože dovoluje eliminovat faktor pohlaví i věkovou heterogenitu souborů (tzv. normalizování dat).

[ na obsah ]